Mulţimea finită S = S1 x S2 x... x Sn se numeşte spaţiul soluţiilor posibile (este un produs cartezian). Soluţiile posibile care satisfac condiţiile interne se numesc soluţii rezultat. Ceea ce ne propunem este de a determina toate soluţiile rezultat, cu scopul de a le afişa sau de a alege dintre ele una care maximizează sau minimizează o eventuală funcţie obiectiv dată.
O metoda simplă de determinare a soluţiilor rezultat constă în a genera într-un mod oarecare toate soluţiile posibile şi de a verifica dacă ele satisfac condiţiile interne. Dezavantajul constă în faptul că timpul cerut de această investigare exhaustivă este foarte mare. Astfel, chiar pentru |Si| = 2, " i, timpul necesar este de ordinul 2n, deci exponenţial.
Metoda backtracking urmăreşte să evite generarea tuturor soluţiilor posibile. În acest scop, elementele vectorului X primesc pe rând valori în sensul că lui xk i se atribuie o valoare numai dacă au fost atribuite deja valori lui x1 ,... xk-1 . Mai mult, odată o valoare pentru xn stabilită, nu se trece direct la atribuirea de valori lui xk+1 , neîndeplinirea lor exprimând faptul că oricum am alege xk+1,...,xn nu vom putea ajunge la o soluţie rezultat, adică o condiţie pentru care condiţiile interne să fie satisfăcute.
Evident că în cazul neîndeplinirii condiţiilor de continuare va trebui să facem o altă alegere pentru xk sau dacă Sk a fost epuizat să micşorăm pe k cu o unitate încercând să facem o nouă alegere pentru xk etc.; această micşorare a lui k dă numele metodei, ilustrând faptul că atunci când nu mai putem avansa, urmărim înapoi secvenţa curentă din soluţie. Este evident că între condiţiile de continuare şi condiţiile interne există o strânsă legătură. O bună alegere pentru condiţiile de continuare are ca efect o importantă reducere a numărului de calcule.
Metoda backtracking poate fi reprezentată uşor, pe un arbore construit astfel:
- nivelul 1 conţine rădăcina;
- din orice vârf de pe nivelul k pleacă sk muchii spre nivelul k+1 etichetaţi cu cele sk muchii ale lui Sk.
Nivelul n+1 va conţine s1 × s2 × ... × sn vârfuri. Pentru fiecare vârf de pe nivelul n+1, etichetele muchiilor conţinute pe drumul ce leagă rădăcina de acest vârf reprezintă o soluţie posibilă.
Exemplu - Să considerăm problema submulţimilor de sumă dată care constă în următoarele: Fie A = (a1, a2, ..., an) cu ai > 0, " i. Fie MÎR+. Se caută toate submulţimile B ale lui A pentru care suma elementelor este M.
Pentru a putea realiza problema prin metoda backtracking vom reprezenta soluţia sub forma x = (x1, ..., xn) unde xi = 1 dacă aiÎB şi xi = 0 în caz contrar. Sa ne situăm în ipoteza ca n=4. Arborele ataşat metodei backtracking este următorul:
Câştigul obţinut prin introducerea condiţiilor de continuare constă în faptul că, dacă într-un vârf ele nu mai sunt verificate, se va renunţa la parcurgerea subarborelui care are ca rădăcină acest vârf.
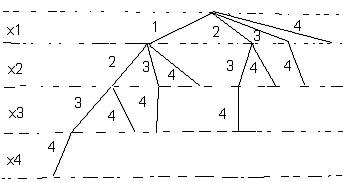
Acest exemplu permite prezentarea unei variante a metodei backtracking. Într-adevăr, să considerăm drept soluţie posibilă o valoare k £ n împreună cu k-uplul (x1, ..., xk) unde pentru i Î {1, ..., k}, xi reprezintă indicele elementului pe care îl introducem în B. Evident xi ¹ xj pentru i¹j. Pentru a nu se repeta soluţii, vom presupune x1<x2<...<xn .
Obţinem astfel următorul arbore în care fiecare vârf corespunde unei soluţii posibile.
Niciun comentariu:
Trimiteți un comentariu